■MT法とは
MT法は目的に対して均質なデータを単位空間として定義し、未知データの単位空間の中心からの距離をマハラノビスの距離(MD値)として求める方法です。複数の項目から判定できることが特徴です。
マハラノビスの距離(MD値)の算出方法
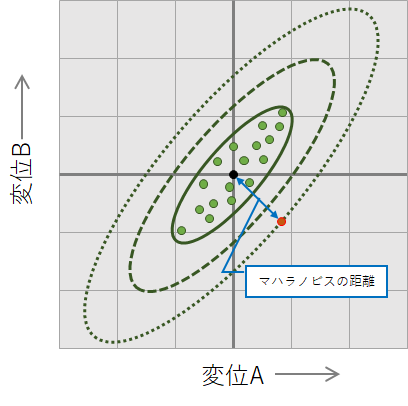
均質なデータ(緑プロット)を群とし単位空間として利用します。
未知データ(赤プロット)が単位空間からどの程度離れているかの度合いによって定量的に均質データとの差異を求めます。
左図は変位が2つのイメージですが、多項目の場合は、項目間ごとにマハラノビスの距離(MD値)を求め、平均値を算出することで多項目においての単位空間からの離れ度合いを評価します。
■標本線とは
MT法は多項目でも計算ができますが、振動や温度、圧力などの時系列に変化するデータをそのまま計算することができません。
標本線を用いることで、時系列に変化するデータを、変化量と存在量に変換することができます。

標本線は時系列に変化するデータ(黒線)に横線として配置し、交点の数を変化量、交点から交点までの距離を存在量としてグラフ全体を数値で表す方法。
標本線の上下配置や本数によって単位空間が形成されるため、標本線の上下への配置や本数を適切に配置することが求められます。
Signal Catcherでは標本線から存在量と特徴量をより正確に抽出する内部処理アルゴリズムを搭載しています。
■重心法とは
標本線と同じく、時系列に変化するデータを、区間で定義された重心位置(x,y)に変換した数値を特徴量とする方法です。

重心を定義する区間を決め、それぞれの区間で重心を算出する方法。
重心法は大まかな波形のうねりをとらえることに優れてることが特徴です。
区間によって算出される重心の値によって単位空間が形成されるため、正常と異常を判別しやすい範囲を適切に設定することが求められます。
■遺伝的アルゴリズム(GA法)とは
遺伝的アルゴリズム(Genetic algorithm、略称:GA)は近似解を求める手法。
変位する項目に解の候補を入力した個体を複数用意します。個体はそれぞれ変位する項目を遺伝子として数値で表現し、適応度の高いものが優先的に選択され、それら選択された個体の遺伝子に交叉や突然変異などの操作を行い、第2世代の個体を生成します。適応度の低いものは次世代へ引き継がれず淘汰されます。この操作を繰り返すことで近似解を探索していきます。
例題「サラリーマン巡回問題」
下の図は富山県の15か所(水色プロット)をすべて通るための順番のうち、移動距離が最も短くなるものを遺伝的アルゴリズムで解を求めたものです。
順列問題となり、組合せ総数は653,837,184,000通りもあります。
左図は道順を表しており、右のグラフは縦軸に移動距離、横軸に世代数を表しています。
遺伝的アルゴリズムを用いることで6,538億通りという途方もない移動距離を計算せずに、短時間で最適解に近い解を求めることができます。
計算の特性として、第一世代の集団の特性や交叉、突然変異の操作に影響されて解が選択されるため、最適解を得ることは難しいですが短い時間で近似解を導出できることが特徴です。
Signal Catcherでは、このアルゴリズムを利用して標本線位置を最適化しています。

